Un challenge intense
Quatre jours, quatre nuits et quatre signaux temporels ! Notre équipe réussira-t-elle à détecter les anomalies en compétition avec les autres groupes ?
En début de M2, j’ai participé à un Hackathon de l’Unistra. J’y ai dirigé une équipe sur les 4 jours du challenge. Nous avons travaillé sur de l’anomaly detection dans des séries temporelles.
L’objectif
Le défi consistait en ceci : nous disposions des signaux A, B, C, E et F. Nous savions que le signal A était sain et que parmi B, C, E et F, un autre signal était également indemne. Notre tâche était de trouver ce second signal sans défaut, puis d’identifier combien de types d’anomalies différentes se trouvaient dans les signaux défectueux.
Contexte
Avant ce Data Challenge, nous avions très peu de connaissances en IA. Nous avons donc consacré tout notre temps libre à nous former à l’aide de ressources en ligne. De plus, durant tout le challenge nous avons choisi de travailler avec les outils de MatLab.
Extraction des données
Initialement nous étions parti pour utiliser nos différents outils sur les signaux temporels. Cependant après plusieurs échecs, nous avons compris que ces signaux étant trop similaires il est difficile sinon impossible d’y détecter les anomalies.
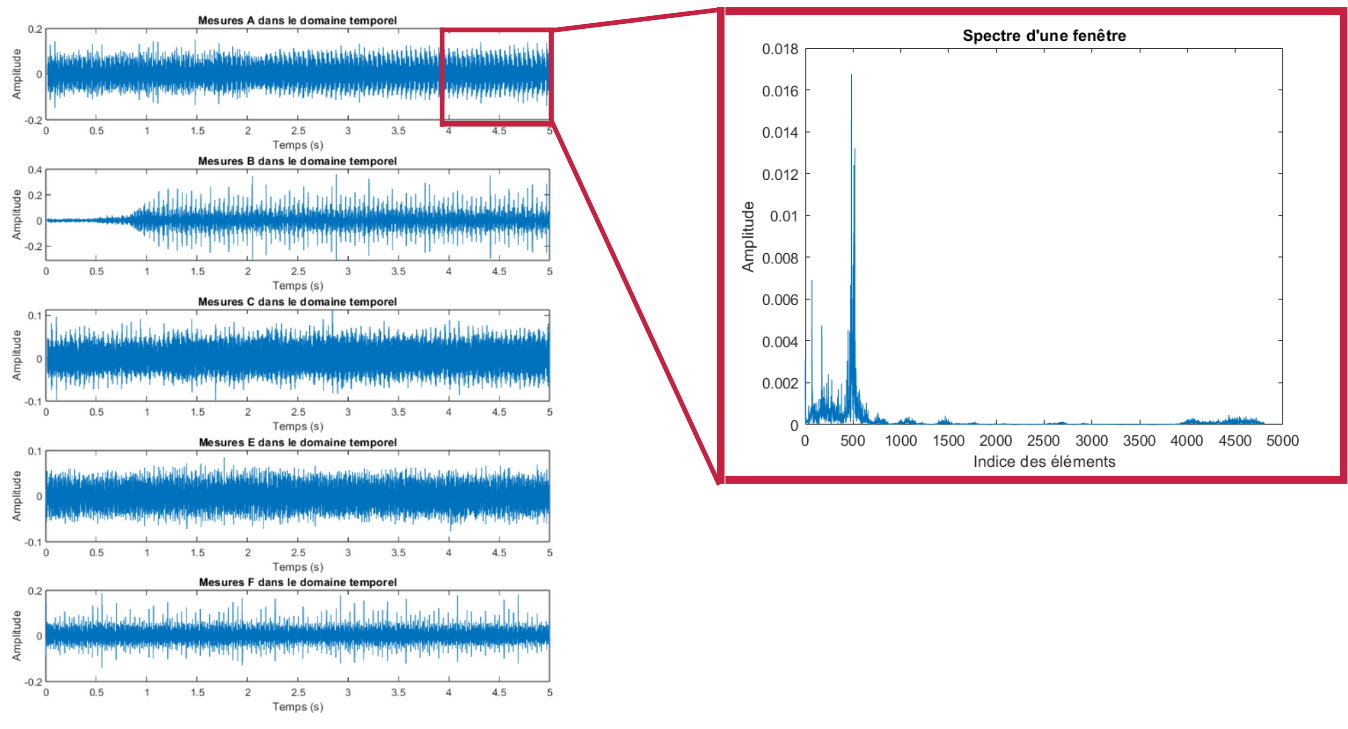
Cependant en passant dans le domaine fréquentiel, rien qu’à l’oeil nu on voit que les signaux présentent des composantes fréquentielles bien différentes. Détecter des anomalies devient donc possible.
Choix de la fenêtre glissante
En passant dans le domaine temporel, il est possible de segmenter les signaux en plusieurs fenêtres. Cette approche permet de disposer d’une quantité suffisante de données pour l’entraînement du modèle. En effet, en divisant le signal en 5, 10, 50 ou 100 fenêtres, on peut considérablement augmenter le volume de données disponibles.
Cependant, cela pose un dilemme. Si le nombre de fenêtres est trop faible, le modèle risque de souffrir d’underfitting, ce qui entraînera un manque de précision. À l’inverse, si le nombre de fenêtres est trop élevé, chacune d’entre elles sera trop petite, ce qui entraînera une résolution spectrale trop élevée et rendra les défauts difficilement détectables.
De manière empirique, nous avons opté pour un découpage en 50 fenêtres avec un recouvrement spectral de 50 % (chaque fenêtre est décalée de la moitié de sa taille).

Features calculées
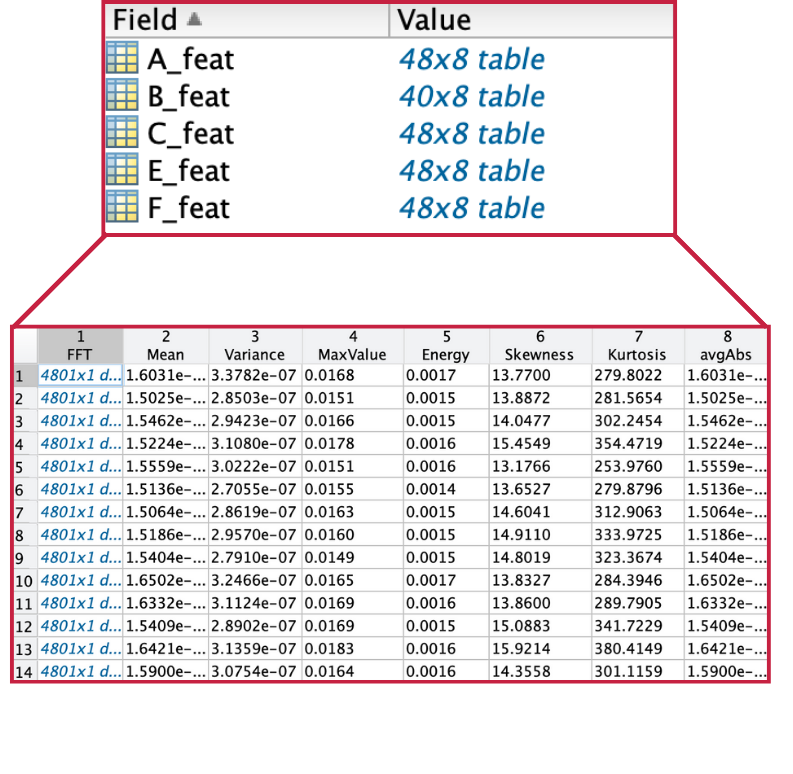
Même si, pour certaines méthodes, nous avons utilisé directement les spectres de fréquence, nous avons également extrait plusieurs caractéristiques des spectres, telles que : la moyenne, la variance, les valeurs maximale et minimale, l’énergie, la skewness, la kurtosis et la moyenne des valeurs absolues.
Méthodes
LSTM Forecasting
Le LSTM (Long Short-Term Memory) forecasting est une technique de prédiction basée sur les réseaux de neurones récurrents (RNN), conçue pour traiter et prévoir des données séquentielles.
- Nous avons donc entraîné un réseau LSTM en utilisant une répartition 80/20, soit 80 % des données du signal A pour l’entraînement et 20 % pour le test.
- Nous avons ensuite cherché à prédire les spectres, que nous avons comparés aux spectres mesurés.
- En calculant l’erreur (Area under Curve, AuC) et en appliquant un seuil, il est possible de déterminer quels signaux sont défectueux.

On voit bien que la reconstruction se fait correctement et que pour le signal A, l’erreur est très faible. Et alors en calculant l’AuC de la RMSE, on obtient le classement suivant :
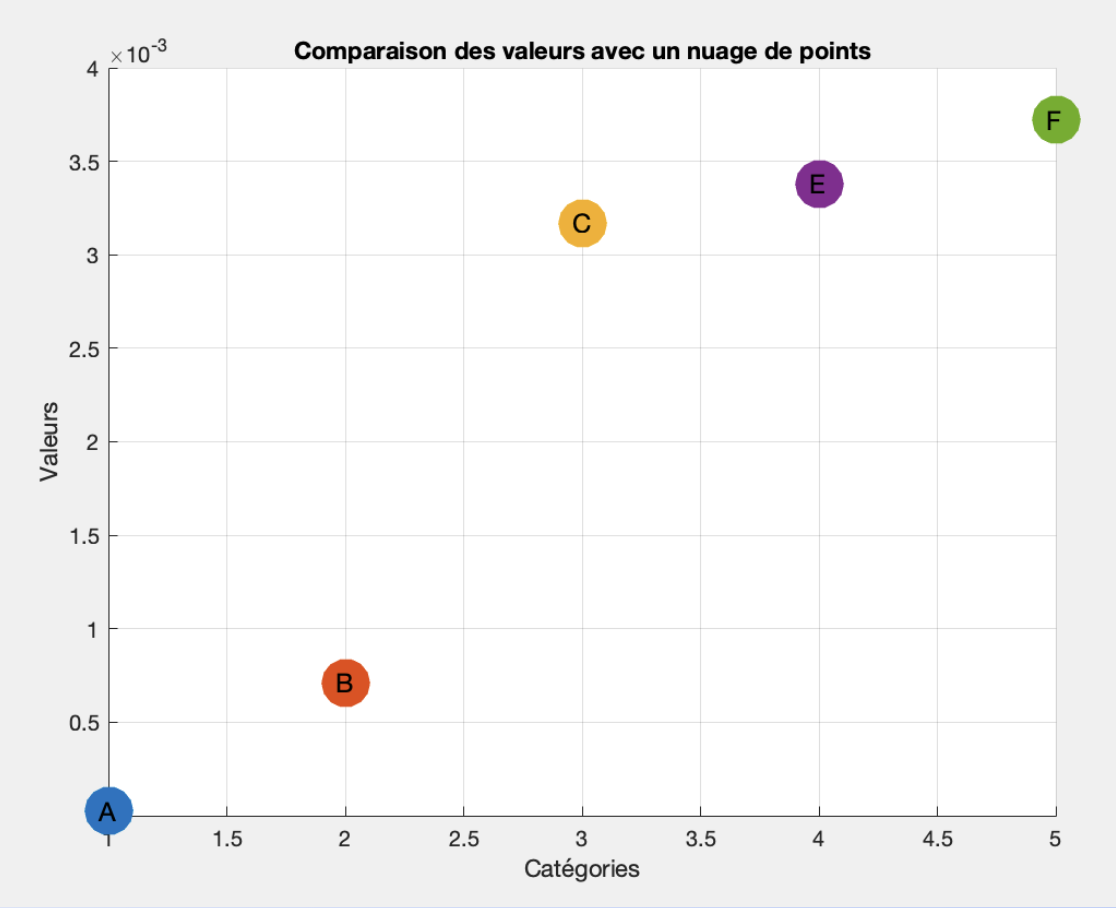
Donc pour conclure, avec cette méthode, nous déterminons que le signal B est le signal sain parmis tous les signaux.
LSTM AutoEncoder
Le LSTM autoencoder (AE) est un modèle de réseau neuronal combinant des LSTM pour encoder et décoder des séquences temporelles. Il apprend à compresser les données d’entrée en une représentation réduite (encodage), puis à les reconstruire (décodage).
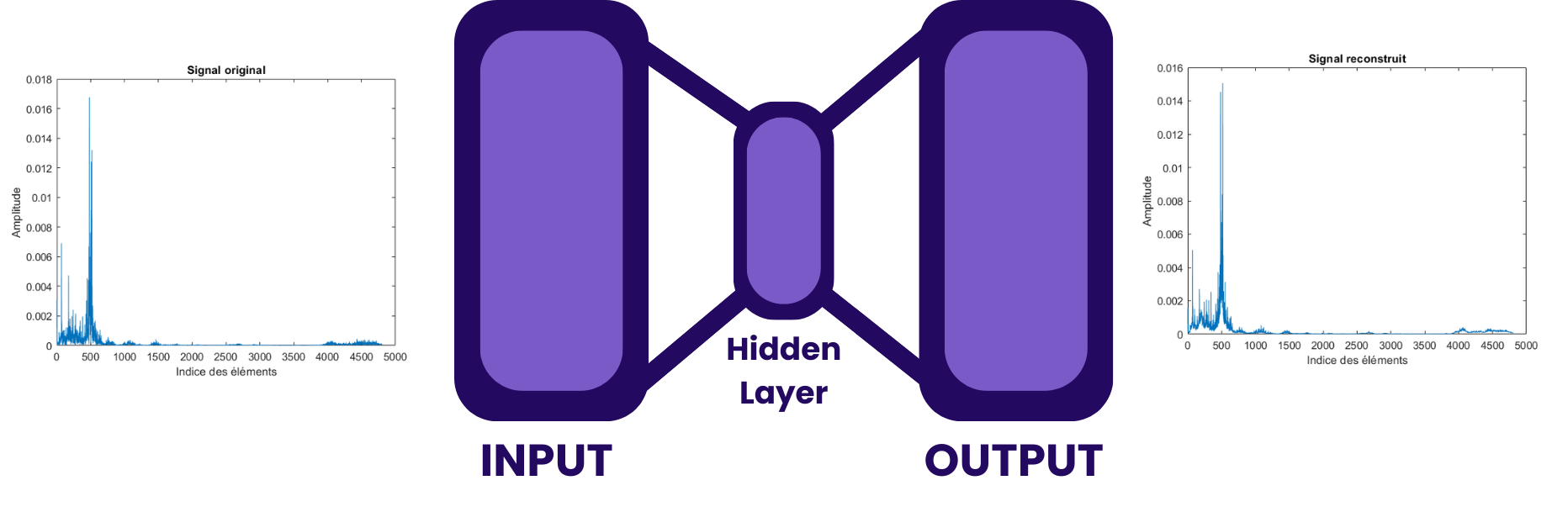
Cette fois au lieu de fournir à l’AE directement les spectres de fréquences comme pour le LSTM-forecaster, nous avons fourni les features de ces fenêtres.
Voici les résultats que nous obtenons :
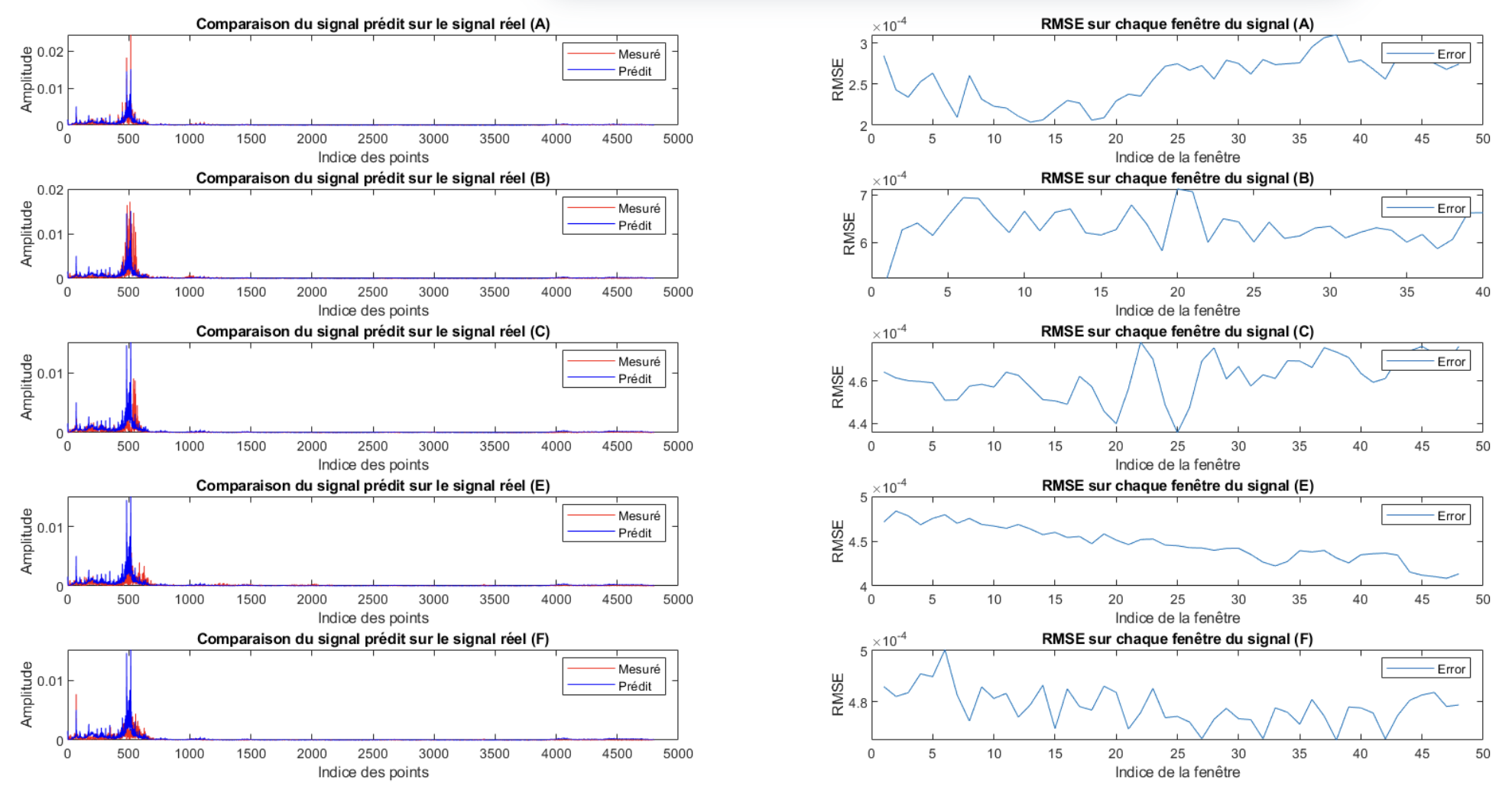
Nous observons que l’AE parvient bien à reconstruire le signal A et décèle des fautes dans les autres signaux. Cependant, étant donné la complexité d’application de cette méthode, nous n’avons pas eu le temps de comparer les RMSE moyenne de tous les résultats ce qui fait que cette méthode ne nous a donné aucun résultat exploitable.
Clustering (K-means)
Le clustering par K-means est une méthode de regroupement non supervisée qui divise les données en K clusters distincts. Chaque point de données est affecté au cluster dont le centre (centroïde) est le plus proche, et les centres sont mis à jour itérativement jusqu’à stabilisation.

Cette méthode avait un double objectif. D’une part, classer l’ensemble des signaux en deux clusters afin de distinguer les signaux corrects des défectueux. D’autre part, en sélectionnant les bonnes caractéristiques (features) et en déterminant le nombre optimal de clusters, nous espérions identifier les signaux présentant les mêmes types d’erreurs.
Nous avons donc effectué le clustering en utilisant directement les points des FFT comme feature. On a donc plusieurs milliers de features par échantillon. Voici les résultats (sachant que chaque signal a été décomposé en environ 50 fenêtres et que les fenêtres sont classés respectivement A-B-C-E-F):
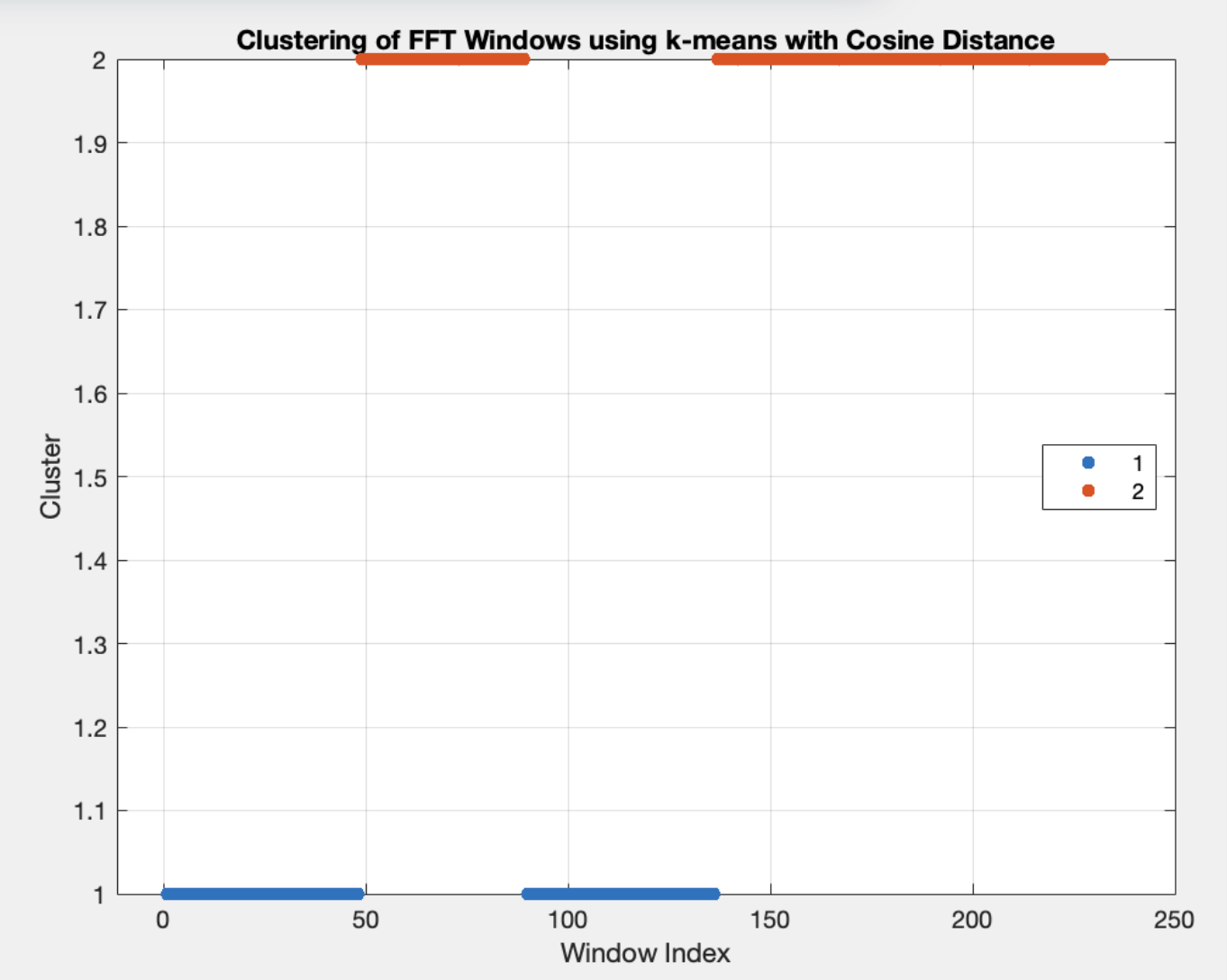
Ci-dessous est représenté le premier résultat que nous avons eu. Il nous dit que le signal C serait le bon signal. Cependant, étant donné le grand nombre de features il était possible que nous soyions en overfitting. Ce faisant, nous avons procédé à une PCA (Principal Component Analysis). Ainsi de 9000 feautres, on passe à 111.
Et cette fois, voici les résultats :
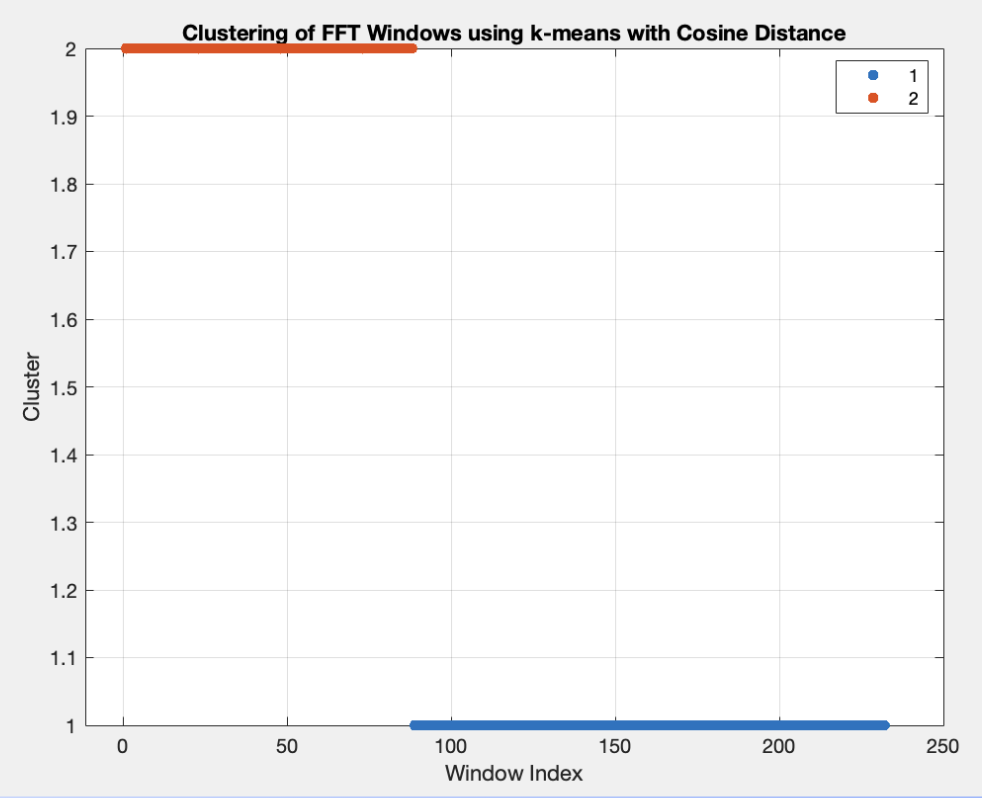
Cette fois on obtient le signal B ce qui corrobore nos résultats précédents.
Nous avons également fait un clustering cette fois sur les feautres et nous avons fait 3 clusters. Nous espérions ainsi détecter les types d’erreur. Voici ce que nous obtenons :

Nous observons alors à nouveau que le signal B est le signal sain (similaire à A). Mais nous voyons également que C et F ont une anomalie qui est classée dans le même cluster.
Nous concluons que le dataset dispose de 2 types d’erreur et que le signal sain est le signal B
Bilan
Ce Hackathon a été une expérience intense et formatrice, où nous avons su tirer parti de diverses techniques d’intelligence artificielle, malgré nos connaissances initialement limitées. En combinant analyse fréquentielle, réseaux LSTM et clustering K-means, nous avons pu identifier avec succès le signal sain et classer les anomalies.
En conclusion, ce concours m’a permis d’acquérir des compétences dans l’utilisation de diverses techniques de détection d’anomalies sur des séries temporelles. Pour la suite de mes études, j’ai l’intention de continuer à me former et me spécialiser dans ce domaine, qui a fortement éveillé mon intérêt.
